
Ein sehr beliebtes Thema in der Algebra ist die Problemlösung in einem rechtwinkligen Dreieck mit dem Satz des Pythagoras . Der Satz ist eine einfache Formel, die die Beziehung zwischen den Seiten jedes rechtwinkligen Dreiecks zeigt. Grundkenntnisse in Quadrat und Quadratwurzel sind erforderlich. Wenn Sie lernen wollen , den Satz des Pythagoras zu beweisen , vergessen Sie nicht, diesen Artikel aus einem HowTo zu lesen.
Ein rechtwinkliges Dreieck ist einfach ein Dreieck, das einen rechten Winkel (90º) enthält. Die längste Seite heißt Hypotenuse und wird oft als “c” bezeichnet. Die anderen Seiten heißen Beine und sind “a” und “b” zugeordnet.
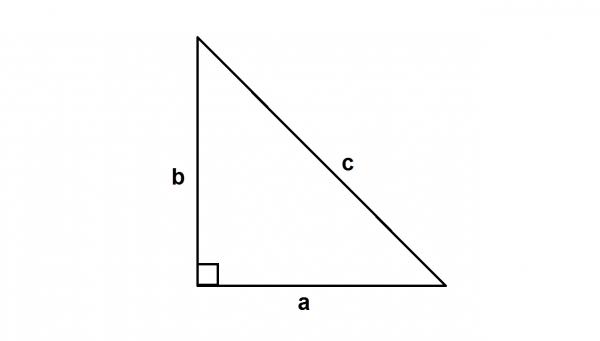
Angenommen, Sie haben Ihr Dreieck auf die gleiche Weise aufgerufen, gilt das folgende Theorem. Das heißt, das Quadrat auf der Seite “a” plus das Quadrat auf der Seite “b” ist gleich dem Quadrat auf der Hypotenuse “c”.
a² + b² = c²
In einem Problem mit rechtwinkligen Dreiecken erhalten Sie normalerweise den Wert von zwei ihrer Seiten, und Sie müssen immer den Wert der fehlenden Seite finden. Es kann einer der drei sein, also müssen wir uns daran erinnern, in der Formel richtig zu ersetzen.
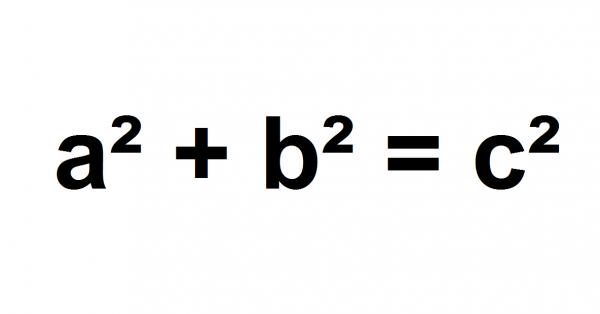
Angenommen wir haben ein Dreieck mit den Beinen der Länge 3 und 4 und wir müssen die Hypotenuse finden. In diesem Fall ist unsere fehlende Seite das “c”. Sehen Sie sich die obige Formel an. Der erste Schritt ist die Substitution, in diesem Fall die Werte, die wir von “a” und “b” kennen. Der nächste Schritt besteht darin, die Quadrate zu berechnen.
Wir kennen den Wert von “c” immer noch nicht. Wir wissen nur, dass c² = 25 und wir sollten uns daran erinnern, dass die Quadratwurzel von x² x ist.
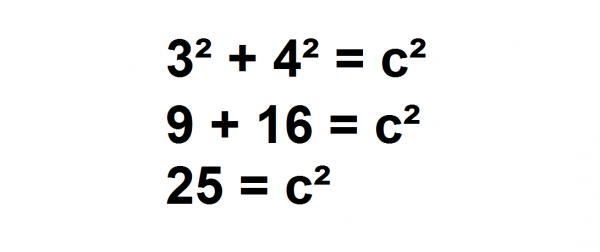
Wie wir bereits im vorigen Schritt gezeigt haben, kehren Sie in der Mathematik zu der ursprünglichen Zahl zurück, wenn Sie die Quadratwurzel eines Quadrats verwenden. Dies liegt daran, dass das Quadrat und die Quadratwurzel inverse Operationen sind. Sie machen einander rückgängig, sie sind “durchgestrichen”.
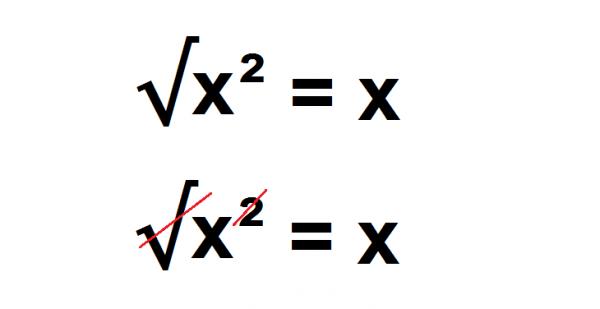
Da wir den Wert von “c” und nicht von c² wollen, geht die Wurzel von “c” mit dem Quadrat, und wenn wir die Wurzel von 25 berechnen, erhalten wir, dass der Wert von “c” 5 entspricht.
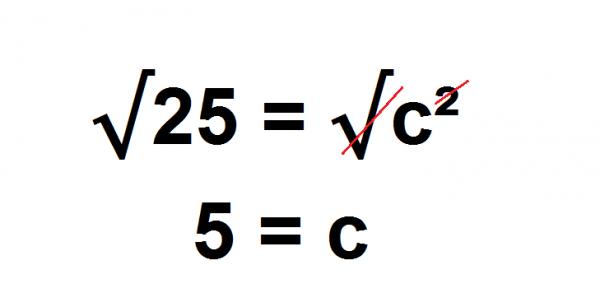
Und wenn Sie überprüfen wollen, ob Sie es richtig gemacht haben, müssen Sie nur die Werte der Beine und der Hypotenuse in der Anfangsformel des Satzes des Pythagoras ersetzen und die Berechnung der Quadrate durchführen:
a² + b² = c²
3² + 4² = 5²
9 + 16 = 25
25 = 25
In der Tat haben wir das Problem gut gelöst und dies wird durch den Satz des Pythagoras bewiesen.
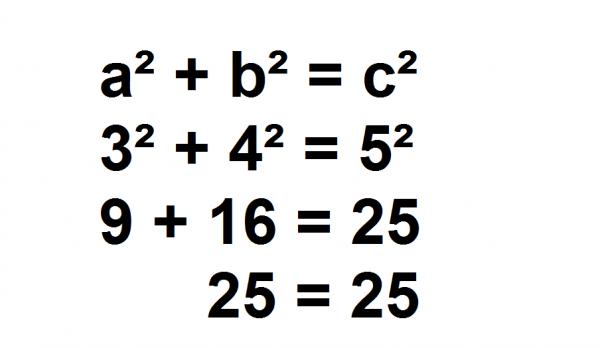
Wenn Sie weitere Artikel lesen möchten, die dem Satz des Pythagoras ähnlich sind, empfehlen wir Ihnen, unsere Trainingskategorie einzugeben.