Wie man das Gebiet aus einem Kreis herausholt

Um im Detail zu erklären, wie man die Fläche aus einem Kreis herausholt, nehmen wir ein Beispiel, damit es klarer und einfacher gesehen werden kann. Nehmen wir an, dass die Aussage der Übung uns dazu auffordert:

Finde die Fläche eines Kreises mit einem Durchmesser von 38 Zentimetern.

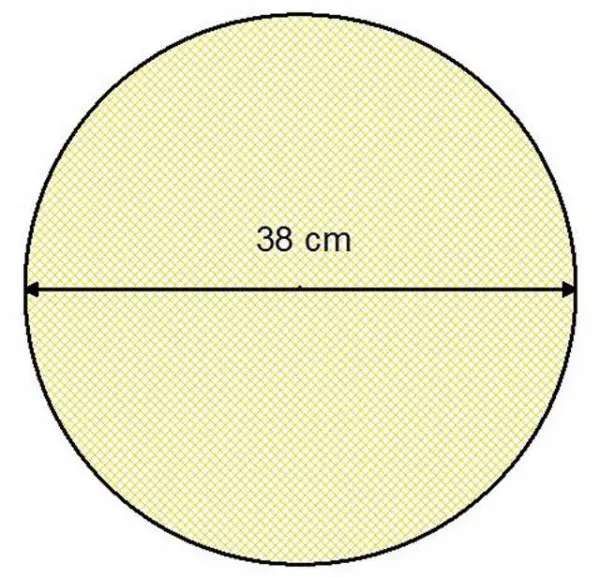
Auf diese Weise müssen wir den Radius eines Kreises berechnen , dessen Durchmesser bekannt ist – der Abstand von einem Ende zum anderen des Kreises – und dazu müssen Sie wissen, dass der Radius gleich dem Durchmesser geteilt durch 2 ist, das heißt, der Radius misst die Hälfte als der Durchmesser.

Mathematisch wäre die Formel:

r = D / 2

r = 38/2 = 19 cm

Sie sollten auch wissen, dass die Formel zum Ermitteln der Fläche des Kreises gleich Pi pro Radius im Quadrat ist:

A = Πr²

Nun, da Sie den Wert des Radius kennen, wissen Sie, wie viel die Pi-Zahl wert ist ? In der Tat, selbst wenn es eine unermessliche irrationale Zahl ist, können wir ihren Wert auf 3,14 angleichen und die mathematische Formel anwenden, die unserem Beispiel folgt:

A = Π × 19² = Π × 361 = 3,14 × 361 = 1133,54 cm²

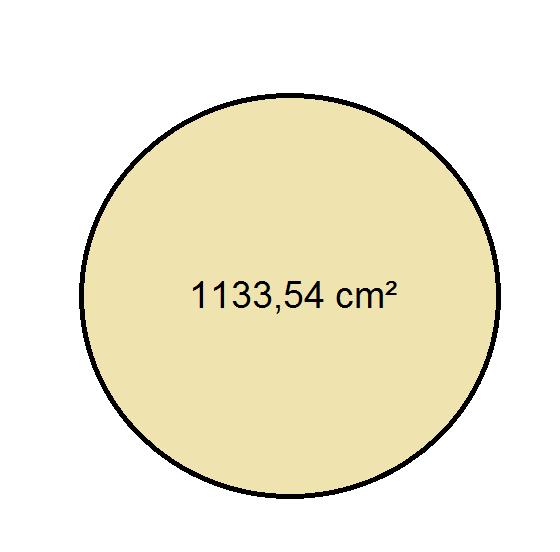
Wie Sie sehen können, ist die Formel zum Entfernen der Fläche eines Kreises einfach, leicht zu merken, und Sie benötigen nur die Daten des Radius des Kreises. In den mathematischen Problemen, bei denen Sie die Fläche eines Kreises finden müssen, werden Sie in der Regel vermeiden, Ihnen das Maß des Radius zu geben. Aus diesem Grund ist es notwendig, auch zu lernen, wie Sie es finden.

Wenn Sie weitere Artikel lesen möchten, die dem Bereich “Aus Kreisen” entsprechen , empfehlen wir Ihnen, unsere Kategorie ” Training ” einzugeben.