Die Höhe eines Dreiecks kann auf verschiedene Arten gefunden werden, abhängig von der Art des Dreiecks und der Information, die Sie haben oder messen. Rechte Dreiecke, die einen Winkel von 90 Grad einschließen, sind am einfachsten mit dem Satz des Pythagoras (wenn die Längen zweier Seiten bekannt sind) oder der Formel der Fläche (wenn die Fläche und die Basis bekannt sind) zu messen.
Die gleichseitigen Dreiecke, in denen alle Seiten gleich lang sind, und die gleichschenkligen Dreiecke, in denen zwei ihrer Seiten gleich lang sind, können in zwei Hälften geschnitten werden, wodurch zwei rechte Dreiecke entstehen. Schräge Dreiecke, die keinen Innenwinkel von 90 Grad haben, sind schwieriger und erfordern Trigonometrie, um ihre Höhe zu finden. Als Nächstes berechnen wir die Höhe eines rechtwinkligen Dreiecks mithilfe der Flächenformel.
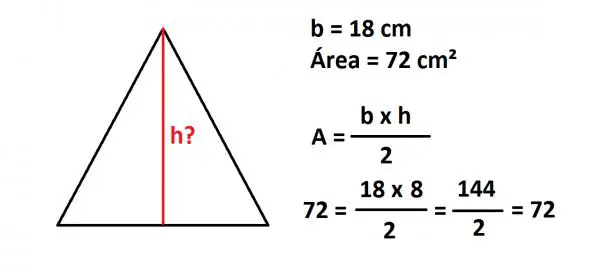
Das erste, was Sie tun müssen, um die Höhe eines Dreiecks zu berechnen , dessen Fläche Sie kennen, besteht darin, das Dreieck zu zeichnen und auf die Seiten und die bekannten Werte wie Fläche und Seiten zu schreiben.
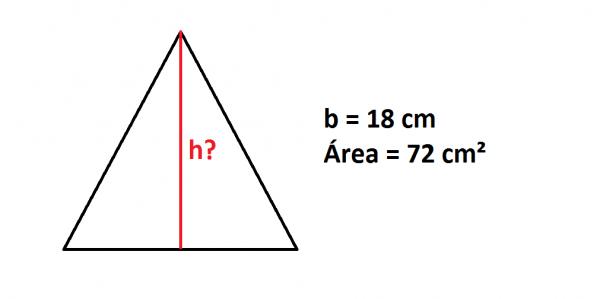
Dann schreibe die Formel der Fläche eines Dreiecks , A = (b · h) / 2, wobei A = Fläche, b = Basis und h = Höhe.
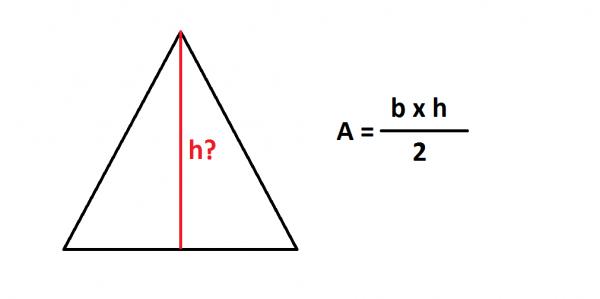
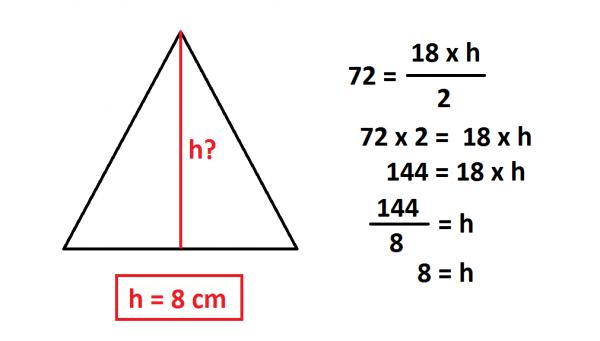
Ersetzen Sie jetzt in der Formel alle Werte, die Sie kennen, also die Fläche und die Basis des Dreiecks, um die Höhe zu finden, damit:
72 (die Fläche des Dreiecks) ist gleich der Multiplikation von 18 mal die Höhe, alle geteilt durch zwei.

Der nächste Schritt wird sein, die h (Höhe) zu löschen, so dass Sie ihren Wert kennen können, denn Sie erinnern sich daran, dass das, was Sie multiplizieren, auf die andere Seite der gleichen Division und der Inversen übergeht.
Also haben wir die 2 geteilt, die sich geteilt hat, um sie mit 72 zu multiplizieren, und wir haben die Operation ausgeführt, und dann werden die 18, die sich multipliziert haben, geteilt. Wenn wir die Berechnungen abgeschlossen haben, entdecken wir, dass der Wert von h 8 ist.
Daher ist die Höhe des Dreiecks 8 cm.
Wenn Sie die Überprüfung durchführen möchten, um sicherzugehen, dass Sie es gut gemacht haben, müssen Sie nur den Wert der Höhe neben denen, die Sie bereits in der Formel wussten, ersetzen, um die Fläche des Dreiecks zu berechnen.
Auf diese Weise erhalten wir, wenn wir die mathematischen Operationen durchführen, dass in beiden Fällen der Wert der Fläche 72 cm² beträgt, also ist es richtig.
Wenn Sie weitere Artikel lesen möchten, die ähnlich sind wie die Höhe eines Dreiecks mithilfe des Bereichs zu kennen , empfehlen wir Ihnen, unsere Kategorie ” Training ” einzugeben.