
Müssen Sie die Fläche einer Pyramide berechnen und wissen nicht wie? Wenn es sich um ein reguläres Polygon handelt, müssen Sie nur die Formel für die Berechnung des Seitenbereichs anwenden und die Fläche der Basis hinzufügen, um die gesamte Basis zu finden. Warten Sie also nicht länger und lernen Sie in diesem Artikel, wie Sie die Fläche der regulären Pyramide berechnen . Es ist sehr einfach, du wirst sehen!
Nehmen wir an, wir haben eine Papppyramide wie die in der Zeichnung, und wir schlagen vor, die Seitenfläche und die Gesamtfläche derselben zu berechnen.
Dazu öffnen wir die Pyramide an einer ihrer Kanten und entfalten sie, bis wir eine flache Figur bekommen. Diese Zahl ist die Entwicklung der Pyramide .
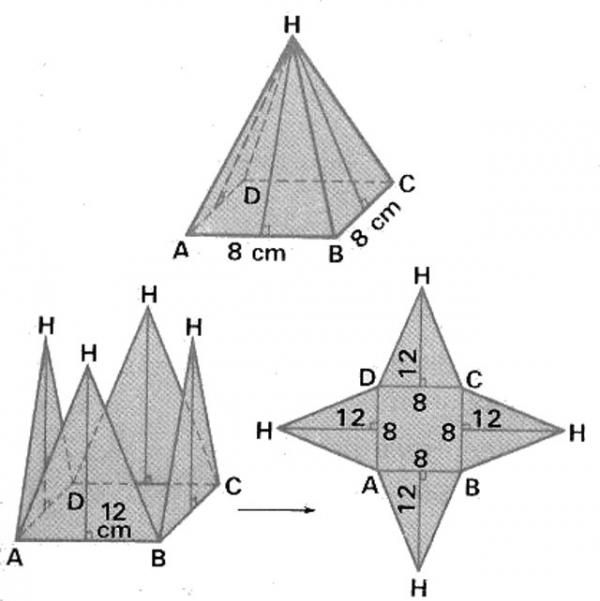
Beachten Sie, dass die Entwicklung der Pyramide durch die Dreiecke gebildet wird, die den seitlichen Bereich und den Grundrahmen bilden. Beachten Sie auch, dass die vier Dreiecke, aus denen der Seitenbereich besteht, gleich sind.
Deshalb:
Seitenfläche der Pyramide = Fläche des Dreiecks ABH x 4
Auf diese Weise wird der erste Schritt darin bestehen, die Fläche jedes der Dreiecke, aus denen die Pyramide besteht, zu bestimmen und dann den Wert mit vier zu multiplizieren.
Aber bevor man die Gesamtfläche kennt, muss man die Fläche jedes Dreiecks nach der Formel finden:
Fläche des Dreiecks = (Basis x Höhe oder Apothem) / 2
Der Seitenbereich einer regelmäßigen Pyramide ist gleich dem Produkt des Umfangs seiner Basis durch das Apothem der Pyramide geteilt durch 2; Denken Sie daran, dass das Apothem die Höhe jedes der Dreiecke ist, die eine regelmäßige Pyramide bilden.
Fläche des Dreiecks = (8 x 12) / 2 = 96/2 = 48 cm²
Nun, da wir die Fläche jedes der Dreiecke kennen, können wir nun den lateralen Bereich der Pyramide berechnen, wie wir im vorherigen Schritt erklärt haben:
Seitenfläche der Pyramide = Fläche des Dreiecks ABH x 4 = 48 x 4 = 192 cm²
Wenn man berücksichtigt, dass die Gesamtfläche der Pyramide die Summe der lateralen Fläche plus der Fläche der Basis ist , kann man unter Verwendung der Messungen des Bildes von Schritt 1 bestimmen, dass:
Fläche der Basis = 8 cm x 8 cm = 64 cm²
Deshalb:
Gesamtfläche der Pyramide = laterale Fläche + Fläche der Basis
Gesamtfläche der Pyramide = 192 + 64 = 256 cm²
Wenn Sie weitere Artikel lesen möchten, die der Berechnung des Bereichs der regulären Pyramide ähneln, empfehlen wir Ihnen, unsere Kategorie Training einzugeben.