Zweidimensionales Array
Sehen wir uns vor dem Einstieg in die Theorie die folgende Tabelle an:
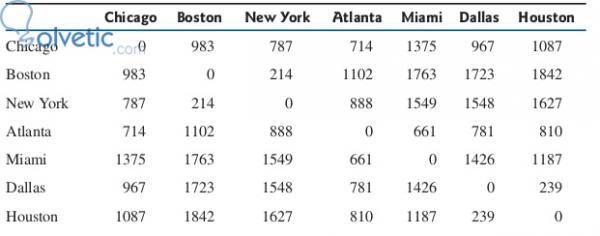
Dies ist ein klassisches Beispiel für eine Matrix oder ein zweidimensionales Array . Wenn wir nach zwei Koordinaten oder Positionen suchen, denen wir einen Wert zuweisen möchten, haben wir im Fall des Bildes die Entfernungen in Meilen von Städten. Wenn wir also in Chicago sind und nach Boston fahren, haben wir eine Entfernung von 983 Meilen. Wenn wir jedes Mal sehen, wenn die Indizes überschritten werden, erhalten wir den Wert. Dies erleichtert unser Leben, wenn wir diese Art von Datenstruktur aufbauen .
Um diesen Effekt in Java zu erzielen, können wir unser Array mit mehr als einer Dimension wie folgt deklarieren:
typeElement [] [] arrayRefVar;
Wenn wir diese Definition nun auf eine Aufgabe in unserem Programm übertragen, bleiben wir wie folgt:
int [] [] array;
Wenn int der Datentyp ist, geben die beiden Klammerpaare [] [] die beiden Dimensionen an, und schließlich ist matrix der Name dieses Elements im Programm. Wir haben dann festgestellt, dass diese Definition fast identisch ist mit der Deklaration eines normalen Arrays, wie wir es bisher gesehen haben.
Kennen Sie die Länge einer Matrix
Diese Operation ist durchaus üblich, um die Länge zu kennen, die wir verstehen müssen. Die grundlegendste Art zu beschreiben ist zu sagen, dass jede Matrix ein Array einer Dimension ist und jedes Element dieses Arrays wiederum ein anderes Array ist , sodass wir das finden können zwei Dimensionen Um seine Länge zu messen, machen wir folgendes:
Zuerst müssen wir die Länge des äußeren Index finden:
x.Länge
Wenn wir das wissen, können wir in jedem Index die Länge des inneren Index suchen:
x [0] .Länge
Es ist nicht so einfach zu sehen, aber sobald wir das Konzept gelernt haben, ist es sehr einfach, damit zu arbeiten. Sehen wir uns das folgende Bild an, das zeigt, was wir gerade erklärt haben:
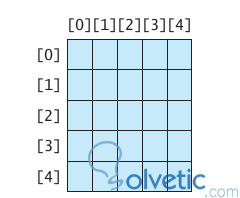
Unser externer Index ist der linke Bereich und unser interner Index ist der oberste . Wir haben also 5 externe Positionen und jede externe Position hat 5 interne Positionen. Wenn wir also die Gesamtgröße unserer Matrix wissen wollen, das heißt, wie viele Nettowerte können wir speichern Wir multiplizieren nur beide Indizes, in diesem Fall können wir 25 Werte speichern.
Damit beenden wir dieses Tutorial. Wir haben uns mit einem Konzept befasst, das etwas komplex zu verarbeiten ist. Dies ist jedoch unabdingbar, da diese Art von Strukturen häufig verwendet wird, insbesondere in neuen Anwendungen, in denen Zugriffskontrollen durchgeführt und zugehörige Werte gespeichert werden müssen an Benutzer.